Experiments for pLEO Satellite Constellations

Research in Industrial Projects for Students (RIPS) is an industrial research program held yearly by UCLA's Institute for Pure and Applied Mathematics (IPAM). Students from around the globe come and work on projects given by industry sponsors. I had the wonderful opportunity to travel to LA, meet some seriously cool people, and write plenty of code in the summer of 2022. My team's project, "Distributed Kalman Filter Designs and Experiments for Proliferated Low Earth Orbit (pLEO) Satellite Constellations," was sponsored by The Aerospace Corporation, a research and development center located in El Segundo, CA.

pLEO constellations, comprised of hundreds to thousands of satellites, are a new type of satellite systems which orbit closer to the Earth's surface than traditional systems. SpaceX's Starlink is just one example of such an implementation, and companies such as Aerosace are interested in the benefits such as lower latency and increased bandwidth.

However, there are a few major drawbacks. A single satellite orbiting the Earth will send a signal to exchange information. This can reach another satellite, or more commonly, a ground station on the surface. Compared to regular satellites, pLEO satellites cover significantly less area since they have a lower orbit radius (aka, a satellite footprint). Building and maintaining ground stations is expensive, so many companies are considering an alternate solution: rather than building enough stations to adequately cover the globe, fix a small number. As a system orbits, only a few satellites at any given time will be within range to exchange information. Finally, allow satellites to communicate with each other for information synchronization.

In particular, my team focused on simulating how satellites could synchronize their clock times. This was not a trivial task, considering things like information latency. For running such simulations, we used Kalman filters and distributed Kalman filters, a state estimation algorithm with many applications in engineering.

The math is somewhat dense (though not exactly complex). In theory: a satellite would estimate its own new information, which introduces noise. Then, it would communicate with other satellites (usually those closest to it) to get more information, which allows it to correct its estimation. Keep doing this over and over, for every satellite in the constellation, and you can model a system through time.

We looked primarily at how the covariance of satellite clock states changed over time. We implemented three algorithms in Python to simulate satellite communication:

1. Naive filter
: assumes any pair of satellites can interact. Infeasible given the constraints, but serves as the base model.
2. Primitive distributed Kalman Filter (PDKF)
: each satellite runs its own filter (or estimation) without accounting for cross-covariances between other satellites.
3. Decentralized Collaborative Localization (DCL) algorithm
: each satellite runs its own filter and approximates cross-covariances whenever it communicates with another satellite.

I wrote the code for the naive filter and PDFK. I also helped develop the scripts which modeled satellite states.

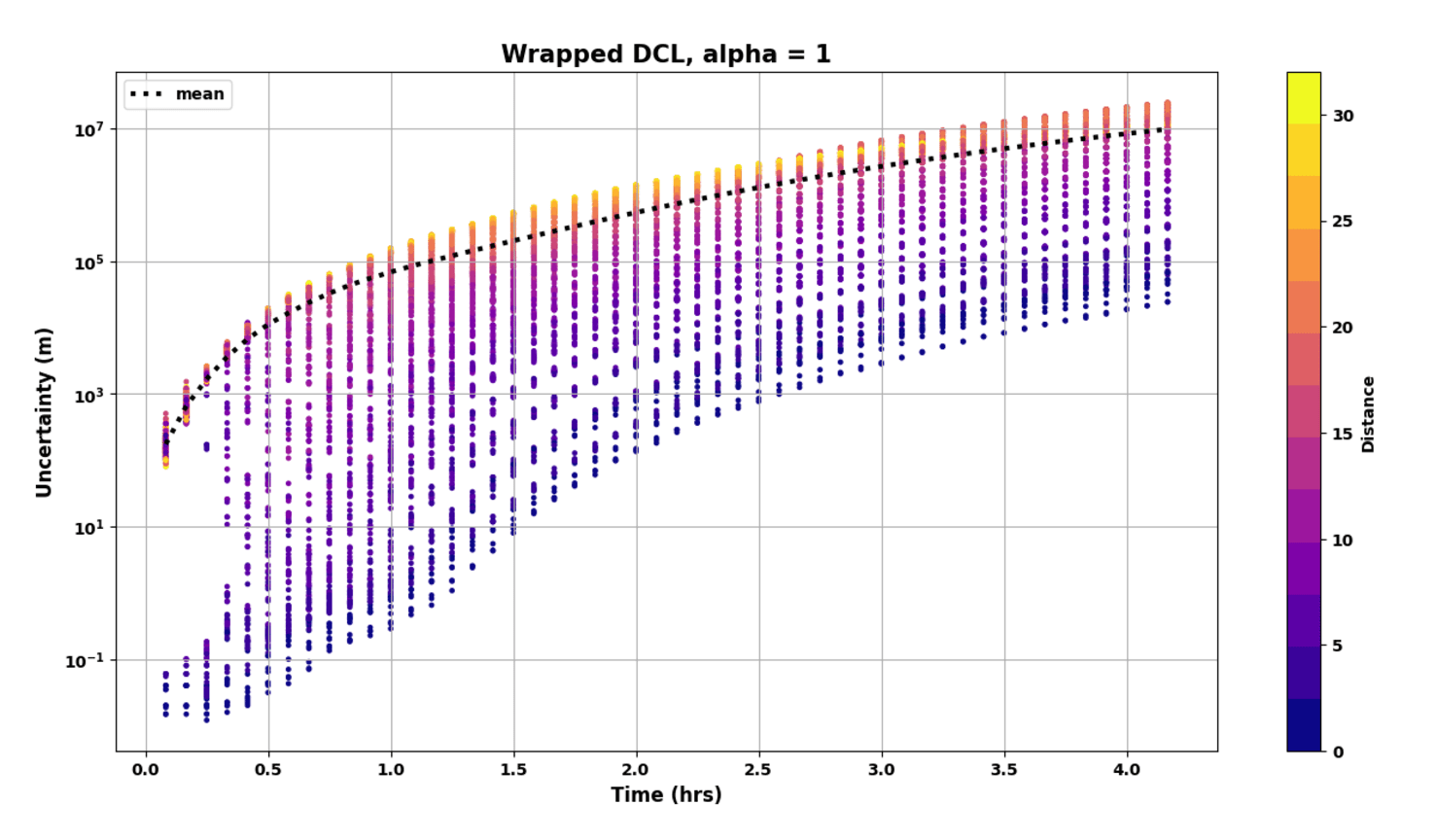
After finishing the code for each filter, we then began experimentation and hypertuning. I primarily tuned the naive filter for noise and initial uncertainty. This, in combination with varying the number of satellites and planes in the constillaton, showed proper tuning could lead to lower values of satellite bias uncertainties. From this, we turned towards tuning the DCL algorithm, where we began to see convergence of satellite uncertainties.

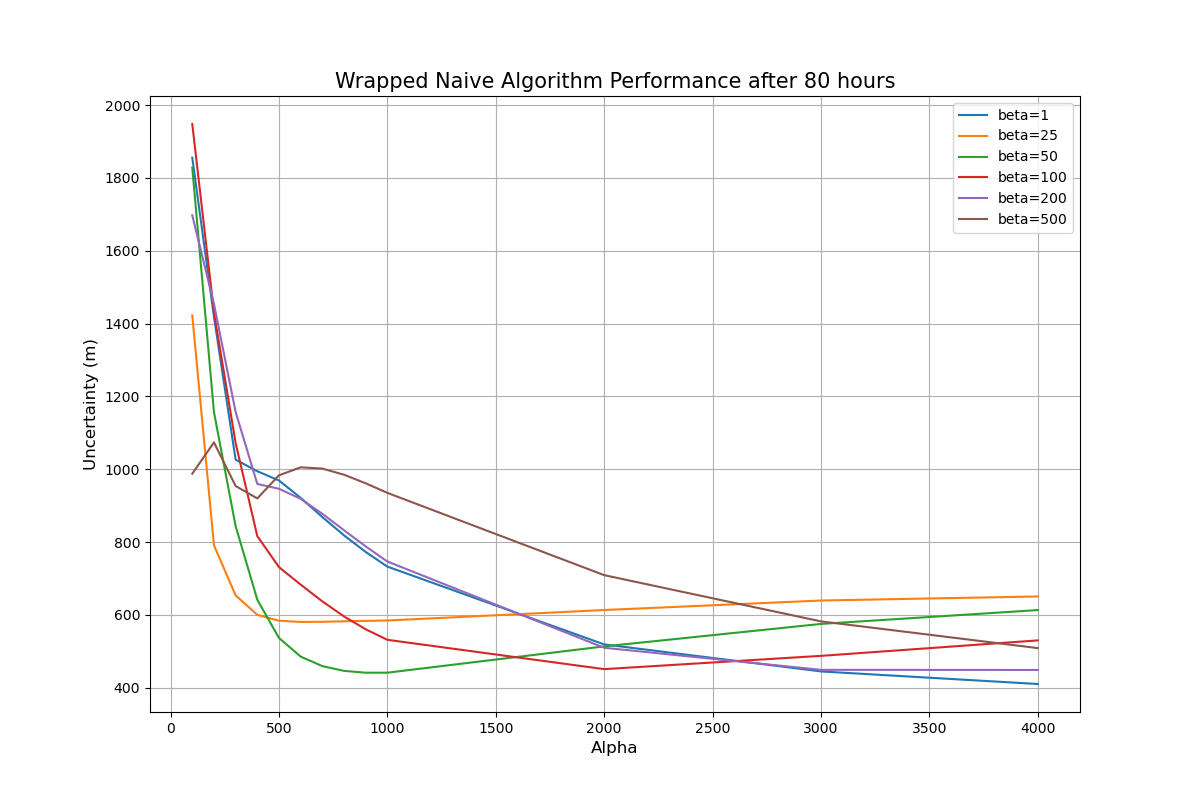
Our other experiments with the DCL algorithm included varying the constellation sizes, limiting communication between certain sets of satellites, and changing the order of satellite communication. We found the best performing communication order was to allow information proprogate outwards from a central satellite which could communicate with the ground. This solution is similar to the process of heat dissipation in a lattice.

At the end of the summer, we summarized our work and results to the Aerospace Corporation and IPAM, in both an outbrief and a final report. For the presentation, I explained each filter and the parameters used in our initial experiments, and reviewed the initial results. In the report, I further laid out the mathematics of each algorithm, and their implementation.

My team presented a poster on our work at the Joint Mathematics Meeting in Boston, January 2023. I also presented solo at the 25th Nebraska Conference for Undergraduate Women in Mathematics later that month:

Check out our poster and results here. For more information about my experiences at these conferences or in LA, check out the links below!